길이 N 짜리 문자열에서 길이 M의 문자열을 검색하는 작업을 O(N+M)에 하는 KMP 알고리즘을 이해하려면,
우선 Failure Function (실패 함수) 를 이해해야 한다.
이 글에서는 Failure Function 에 관한 내용만 작성한다.
길이가 Len 인 문자열 S가 존재한다고 하자. 이 때 S의 index는 1-based 이다.
즉 S[1] ~ S[Len] 까지 문자가 있다. (개인적으로 이 알고리즘은 1-based가 더 직관적으로 이해하기 좋다고 생각한다.)
Failure Function의 정의
1 ~ Len 범위의 수 i 에 대해 F(i) 를 아래와 같이 정의한다.
F(i) := S[1...i] 에서 앞쪽 K자리의 문자열과 뒤쪽 K자리의 문자열이 일치하는 가장 큰 K
(자기 자신은 제외, 즉 K < i )
글로 잘 이해가지 않는다면 아래 그림을 보면 된다.

S[1...1] = "a" 이다. 자기 자신은 답이 될 수 없다고 정의됐으므로 조건을 만족하는 것이 없다. F[1] = 0
S[1...2] = "ab" 이다. 앞쪽 1개, 뒤쪽 1개는 각각 "a", "b" 인데 다르다. 따라서 조건을 만족하는 것이 없어 F[2] = 0
S[1...3] = "aba" 이다. 앞쪽 1개, 뒤쪽 1개는 각각 "a", "a" 이고 일치한다. 이보다 길 수 없으므로 F[3] = 1
S[1...4] = "abaa" 이다. 앞쪽 1개, 뒤쪽 1개가 "a", "a" 로 같으므로 F[4] = 1
S[1...5] = "abaab" 이다. 앞쪽 2개, 뒤쪽 2개가 각각 "ab", "ab" 로 일치하므로 F[5] = 2
S[1...6] = "abaaba" 이다. 앞쪽 1개, 뒤쪽 1개도 일치하지만 앞쪽 3개, 뒤쪽 3개가 "aba"로 같다. F[6] = 3
한 가지 주의할 점은, Failure Function 은 문자열의 절반을 넘어가도 된다는 것이다.

무슨 말인지는 위 그림을 통해 알 수 있다. S = "ababab" 일 때, F[5] = 3, F[6] = 4 이다.
전체 문자열 S 에서 앞의 4개와 뒤의 4개는 "abab"로 일치하기 때문에 F[6] = 4 가 되는 것이다.
앞쪽 4개와 뒤쪽 4개의 문자열이 겹쳐도, 일치한다면 F[i] 의 후보가 될 수 있다는 의미다.
자기 자신은 제외라는 것에 유의하자.
이제 각 i 에 대해 F[i] 를 구하는 과정을 보자.

위 그림에서 우리는 F[1] ~ F[i-1] 까지는 구한 상태고, 이제 F[i] 를 구하고 있는 중이라고 하자.
또한, S[i], 즉 i 번째 문자는 'a' 이다. 그림에서 초록 사각형은 F[i-1] 을 의미하는 것이다.
즉, S[1...(i-1)] 의 앞쪽 사각형과 뒤쪽 사각형이 일치하고, 그것이 최대 길이라는 뜻이다.
만약 그림처럼 S 의 F[i-1] + 1 번째 문자도 S 의 i 번째 문자처럼 'a' 였다면?
우리는 F[i] = F[i-1] + 1 이라는 것을 알 수 있다. 초록 사각형 뒤에 'a'를 붙인 문자열이 S[1...i] 에서 최대가 되기 때문.
하지만, 만약 아래 그림처럼 S의 F[i-1] + 1 번째 문자가 'a' 가 아닌 'b' 였다면?
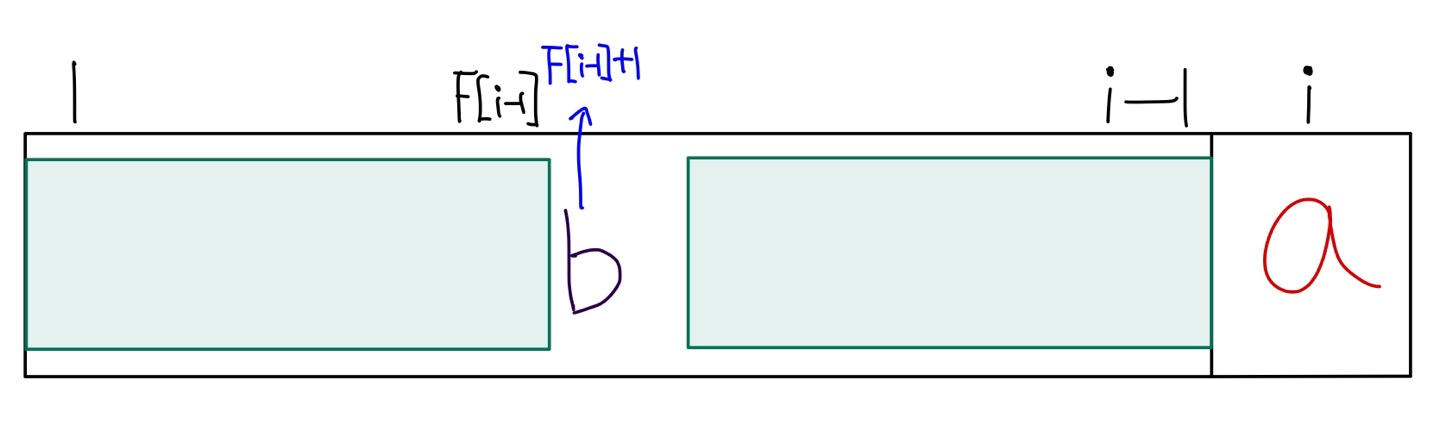
왼쪽 사각형 뒤에 'b'를 붙인 것과, 오른쪽 사각형 뒤에 'a'를 붙인 것이 다르다.
따라서 방금처럼 F[i] = F[i-1] + 1 의 식을 적용할 수 없다.
그렇다면, 한 번 더 들어가서 초록 직사각형에서의 실패함수값을 생각해보자. 이것이 핵심 아이디어다.

앞선 가정에서 우리는 F[1] ~ F[i-1] 을 다 구해놨기 때문에, 초록 사각형에 대한 F 값도 구해놨다.
그림에서 초록 사각형에서의 F 값을 빨간 사각형으로 표시했다.
빨간 사각형의 가로 길이는 몇일까? 즉, 빨간 사각형은 길이 몇 짜리 문자열일까?
여태까지 잘 이해했다면 F[F[i-1]] 이라는 것을 알 수 있다.
초록 사각형의 길이는 F[i-1] 인데, 여기서의 Failure Function이므로 빨간 사각형의 길이는 F[F[i-1]] 이 되는 것이다.
이제 아까처럼 빨간 사각형 옆에 문자 'a'가 있는지 살펴보면 된다.
위 그림처럼 S 의 F[F[i-1]] + 1 번째 문자가 'a' 라면 우리는 F[i] = F[F[i-1]] + 1 로 결정할 수 있다.
빨간 사각형 뒤에 'a'를 붙인 것이 조건을 만족하는 최대 길이 문자열이 되기 때문이다.
만약 빨간 사각형 옆의 문자, 즉 F[F[i-1]] + 1 번째 문자가 'a' 가 아니었다면?
방금 했던 것처럼, 빨간 사각형에서의 실패함수로 또 들어가보고, 그 옆에 'a' 가 있는지 확인하면 된다.
코드는 간단하다. 다른 블로그에 훨씬 간단한 코드가 많지만 나는 직관적으로 이해하기 편하게 짜는 것을 선호한다.
void Failure(){
int i, x;
f[0] = -1, f[1] = 0;
for(i = 2; i <= len; i++){
x = i - 1;
while(x){
if(S[ f[x]+1 ] == S[i]){
f[i] = f[x] + 1;
break;
}
x = f[x];
}
if(!x) f[i] = 0;
}
}
이 코드를 하나하나 해석해보면,
int i, x;
f[0] = -1, f[1] = 0;i 는 말 그대로 우리가 f 값을 구하려는 인덱스, x 는 i 가 정해졌을 때 움직이는 변수다.
사람에 따라 다르지만 나는 f[0] = -1 으로 설정하는 편이다. 그래야 KMP 할 때 좀 더 편하다. 상관은 크게 없다.
어떤 문자열 S 가 와도 f[1] = 0 이기에 초기조건으로 넣어주고 시작했다.
for(i = 2; i <= len; i++){
x = i - 1;f[1] = 0 을 넣어줬기에 f[2] 부터 구하면 된다.
x 는 i-1 부터 시작한다. S[1...i-1] 의 실패함수부터 살펴보기 때문이다.
앞선 설명에 의해 우리는 S 의 f[x] + 1 번째 문자와 S 의 i 번째를 비교할 것이라고 예상할 수 있다.
while(x){
if(S[ f[x]+1 ] == S[i]){
f[i] = f[x] + 1;
break;
}
x = f[x];
}예상대로 S 의 f[x] + 1 번째 문자와, 지금 추가된 S의 i 번째 문자를 비교하고 있다.
만약에 같다면, f[i] = f[x] + 1 이다. 길이 f[x] 짜리 사각형 옆에 S[i] 를 붙인 문자열이라고 생각하면 된다.
그리고 우리는 반복을 끝내야 할 것이다. 최대 길이를 찾았기에 더 작은 단위로 들어갈 이유가 없다.
하지만, 만약 다르다면 x는 더 작은 단위로 들어가봐야 한다.
앞선 설명에서 f[i-1], 즉 초록 사각형 이 안 됐다면 f[f[i-1]], 즉 빨간 사각형을 검사해봤다.
만약 f[f[i-1]] 옆의 문자도 일치하지 않으면 f[f[f[i-1]]] 을 보는 형식의 반복을 계속 해주는 것이다.
따라서 x = f[x] 가 되는 것이다.
만약 x == 0 이라면 더 이상 탐색이 불가능하므로 while 반복문을 종료한다.
if(!x) f[i] = 0;while 문이 끝났는데 x == 0 이라는 것은 S[i]가 포함된 앞뒤 같은 문자열이 없다는 뜻이다.
따라서 f[i] = 0 이 될 수 밖에 없다.
이렇게 f 배열을 채워주고 나면 비로소 문자열을 검색하는 KMP 알고리즘을 실행할 수 있다.
'Algorithm' 카테고리의 다른 글
| Mo's Algorithm (0) | 2022.08.29 |
|---|---|
| Set 와 PBDS (0) | 2022.08.25 |
| CCW 에 대하여 (0) | 2022.08.25 |
| Trie 자료구조 (0) | 2022.08.24 |
| KMP 알고리즘 : 문자열 검색 (0) | 2022.08.19 |



댓글