문제 링크 : https://www.acmicpc.net/problem/14870
실제 전국대회 때 이 문제에 손도 못 댔었는데, 이제야 풀게 되었다.
정말 정말 어렵고, 좋은 문제라고 생각한다.
이 문제는 DP, 누적 합, Fenwick Tree 에 관한 내용을 다 알아야만 풀 수 있다. 풀이도 복잡하다.
1. DP
제일 쉽고 기본적인 관찰은 이 문제는 이차원 DP 를 바탕으로 하는 것이다.
DP[x][y] := x 행 y 열까지의 조개를 주울 때의 최대 개수 로 정의하고,
DP[x][y] = max(DP[x-1][y], DP[x][y-1]) + Cnt[x][y] 라는 간단한 점화식이 나온다.
문제는 Cnt[x][y] 가 쿼리로 바뀌고, 우리는 이를 온라인으로 처리하여 DP 배열값의 총합을 구해야 한다.
2. 관찰 - 같은 행
이 문제에서 제일 중요한 것은 관찰이다. 누적합 및 펜윅트리는 구현 도구에 불과하다.
1번에서 구한 DP 배열의 일부분이 아래와 같다고 가정하자.
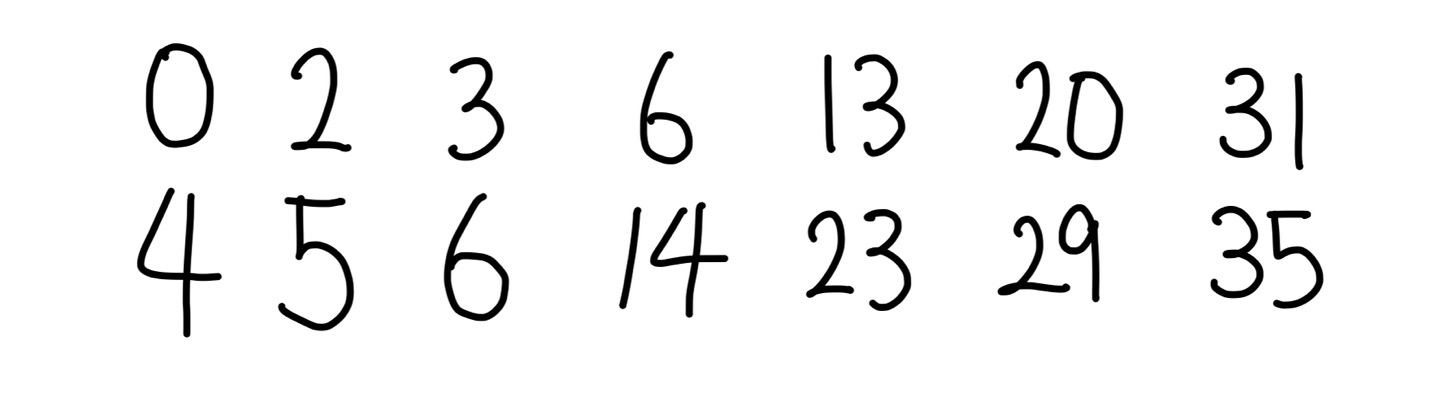
이제, 2행 2열, 즉 5 가 있는 곳의 조개 개수가 1 증가했다고 하자. 당연히 DP[2][2] 도 1 증가한다.

이제, 위 DP 배열은 각 원소의 값이 바뀔 것이다.
우선, 당연한 사실은 1행의 DP 값은 변화가 전혀 없다는 것이다. 그러니 2행의 변화를 보자.
DP[2][3] = 6 은 어디서 왔는지를 보자.
DP[2][2], DP[1][3] 중 DP[2][2] 이 더 크므로, DP[2][3] = 6 은 DP[2][2] 로부터 구해졌다.
때문에, DP[2][2] 에 변화가 생기면 DP[2][3] 는 영향을 받아 1 이 증가해 7이 될 것이다.
DP[2][4] = 14은 어떨까?
DP[2][3], DP[1][4] 은 그 값이 6 으로 동일했었다. 그런데 DP[2][3] 는 영향을 받아 1 증가해 7이 됐다.
따라서 DP[2][4] 은 DP[2][3] = 6 + 1 = 7 의 영향을 받아, 이 역시 1 이 증가할 것이다.
위 로직을 반복하면 아래 그림을 얻을 수 있다.

잘 보면, DP[2][7] 은 그대로 35 로 남게 된다. 왜 그럴까?
DP[2][6] 는 마찬가지로 영향을 받아 1 증가하여 30 이 될 것이다.
그래도 DP[2][7] 입장에서는 그 윗칸인 31 을 선택하는 것이 이득이므로, DP[2][7] 은 갱신되지 않는다.
그러면 DP[2][8 ~ N] 은 어떨까? 즉 8열 부터는 어떻게 될까?
바로 직전, 다시 말하면 왼쪽 칸이 갱신되지 않았고, 윗 행인 1행 또한 갱신이 없으므로 변화가 없을 것이다.
따라서, DP[2][7] 만 영향을 안 받는 것이 아니라, 그 오른쪽으로 쭉 영향을 안 받는다는 것이다.
우리는 같은 행 안에서 영향을 받는 칸들을 찾는 관찰을 마쳤다.
영향을 받는 칸들은 연속적으로 나타난다는 결론을 얻게 되었다.
3. 관찰 - 아래 행
위 예시에서 DP의 2행의 변화는 알아냈으니, 3행으로 넘어가보자.

편의상 8열, 9열을 추가했고, 위에서 확인한 DP[2][2] ~ DP[2][6] 을 1 씩 증가시켰으며, 3행을 추가했다.
이제 3행에서 누가 영향을 받아 1 이 증가할지 살펴보자.

관찰 1을 이해했으면 위 그림을 어렵지 않게 이해할 것이다.
DP[3][2]와 DP[3][3] 은 윗줄로부터 온 값이 아니고, 갱신되지 않은 왼쪽으로부터 온 값이기에, 변화가 없다.
그러나 DP[3][4] 는 DP[2][4] 가 DP[3][3] 보다 커졌으므로, DP[2][4] 의 영향을 받게 되어 1 증가한다.
DP[3][5] = 28, DP[3][6] = 37 은 무조건 영향을 받아 1 증가할 것이다. 왜 그럴까?
DP[3][4] 가 영향을 받게 되었으므로, DP[3][5] 입장에서는 위칸, 왼쪽칸 모두 영향을 받아 갱신된 것이다.
DP[3][5] 는 둘 중 하나로부터 온 것인데, 둘 다 영향을 받은 것이기에, 무조건 영향을 받을 수 밖에 없다.
DP[3][6] 도 마찬가지다.
DP[3][7] 부터 보면 되는 것인데, DP[3][6] 이 DP[2][7] 보다 크니까 영향을 받게 된다. DP[3][8] 도 마찬가지.
그러나, DP[3][9] 는 왼쪽 보다 윗칸이 더 크게 때문에 영향을 받지 않는다.
우리는 3행은 4열 ~ 8열 까지만 갱신이 된다는 것을 알게 되었다.
여기서 중요한 것은 다음 두 가지다.
1. 3행에서 영향 받는 시작점은 2행의 시작점과 같거나, 더 오른쪽에 있다.
2. 3행에서 영향 받는 끝점은 2행의 끝점과 같거나, 더 오른쪽에 있다.
즉, 아래 행으로 내려올수록 영향을 받는 직선구간은 오른쪽으로 밀리는 규칙을 가진다.
일반화 하면 아래 그림과 같다.

이제 관찰이 끝났다.
3. 누적 합
이제 정해에 거의 다 도달했다. 문제를 이를 어떻게 구현할 것인가다.
위 구간을 구한 후 모든 칸에 1 씩 더하거나 1 씩 빼면 당연히 시간초과가 날 것이다.
lazy propagation 을 쓰는 대신, 유명한 누적합 테크닉을 적용하자.
구간 [s, e] 에 +1 을 하는 것은, arr[s]++, arr[e+1]-- 를 한 후 누적합을 구하는 것과 같다.
예를 들어 arr[1] ~ arr[6] 을 1로 만드려면, arr[1] = 1, arr[7] = -1 을 넣어놓고 누적합을 구하면 된다.
즉 모든 구간에 다 1 을 더할 필요 없이, 2개의 칸만 갱신시켜놓으면 된다.
애초에, 1 에서 설명한 DP 배열을 채울 때, 누적합을 적용할 수 있는 형태로 만들고 시작해야 한다.
무슨 말이냐면, 위 예시에서 들은 DP Table 의 2행을 보자.

원래대로라면 위처럼 DP Table 을 채워야 하지만, 이러면 누적합을 적용할 수 없다.
실제로는 아래 박스처럼 DP Table 을 채워야 한다.
그렇게 되면, 누적합을 했을 때 정상적으로 4 5 6 14 23 29 35 가 나오게 된다.
아까 관찰에서, DP의 2행은 2열부터 6열까지 1을 더해주어야 했다. 방금 설명한 테크닉을 적용하자.

2열에 +1, 7열에 -1 을 해주면 4 2 1 8 9 6 5 가 된다.
이것의 누적합은 4 6 7 15 24 30 35 가 되고, 우리가 의도한 대로 5칸에만 1이 더해졌다.
최종 구현의 틀은 아래와 같다.
1. 조개 개수에 관한 NxN 배열을 입력받고, DP Table 을 채운다.
단, DP 값을 그대로 넣지 말고, 위처럼 누적합을 적용할 수 있도록 채운다.
(4 5 6 14 23 29 35 가 아닌 4 1 1 8 9 6 6 으로 채우라는 것이다.)
2. 쿼리 U r c 가 들어왔다고 해보자. (D 는 똑같이 하면 됨)
r 행 c+1 열부터 오른쪽으로 가보면서, r 행에서 갱신되는 칸들의 구간을 확보한다.
윗칸, 왼쪽칸의 DP값, 즉 누적합 값은 Fenwick Tree 로 O(log N) 만에 구할 수 있다.
이렇게 구한 r 행의 갱신 구간을 c 열 ~ d 열 이라고 하자.
아까의 테크닉을 적용해 DP[r][c]++, DP[r][d+1]-- 을 한다. (Fenwick Tree update : O(log N))
또한, 답은 (d - c + 1) 만큼 증가할 것이다.
이제 r+1 행을 보면서, c 열부터 출발하여 언제 처음 갱신되기 시작하는지 본다. 그게 s 열이라고 하자.
r+1 행은 기본적으로 s ~ (d 열의 오른쪽) 까지 갱신이 된다.
따라서, r+1 행을 호출하고, d 열부터 오른쪽으로, 재귀적으로 구간을 확보한다.
최종 시간복잡도는 O(n2 log n) 이다.
댓글